Directx12
- 전자 책 무료로 나와있음 2022.07.28
- 외적 , 직교화 , 점 2022.07.21
- 내적, 직교투영 , 직교화 2022.07.18
- 벡터의 길이와 단위벡터 2022.07.17
- 벡터의 좌표 , 연산 2022.07.15
- 다이렉트12 예제 실행 시 에러 대처 2022.04.18 1
전자 책 무료로 나와있음
외적 , 직교화 , 점
※ 외적(Cross dot 또는 Outer product)
- 외적은 벡터와 벡터를 곱하면 내적과 달리 벡터가 나온다. (내적은 스칼라 값이 나온다.)
오직 3차원 벡터에서만 정의 된다. (2차원은 x)
두 3차원 벡터 u , v를 외적을 취하면 u,v 모두에 직교인 또 다른 벡터 w가 나온다.
- 정의
U x V 일 때


V x U 일때


W가 외적 방향이다.
왼손 좌표계 적용시 두벡터를 반대로 곱하면 새로 나오는 벡터가 뒤집어 진다.

- 계산해보면
U = (2 , 1 , 3) , V = (2 , 0 , 0) 할 때 , W = U x V 와 Z = V x U를 비교하교 직교임을 확인해보자.
W = U x V
W = ( (1 x 0) - (3 x 0) , (3 x 2) - (2 x 0) , (2 x 0) - (1 x 2) )
W = (0 , 6 , -2)
Z = V x U
Z = ( (0 x 3) - (0 x 1) , (0 x 2) - (2 x 3) , (2 x 1) - (0 x 2))
Z = (0 , -6 , 2)
이 결과 U x V ≠ V x U 라는 사실을 알게된다.(외적은 교환 법칙 성립 X)
U x V = -V x U 는 된다.
W가 U또는 V에 직교임을 확인하는 방법은 W●U , W●V 내적을 해서 0이 나오면 서로 직교이다.
- 계산해보면
W●U = WxUx + WyUy + WzUz(공식)
W●U = (0 , 6 , -2) ● (2 , 1, 3)
W●U = (0x2) + (6 x 1) + (-2 x 3) = 0
W●V = (0 , 6 , -2)●(2 , 0 , 0)
W●V = (0x2) + (6x0) + (-2 x 0) = 0
직교임을 알 수 있다.
※ 직교화
- 내적에서 그람슈미트 공정을 통한 직교화를 알아봤다. 여기서는 다른 공정을 통해서 직교화를 구해본다.
다음 공정을 진행한다.

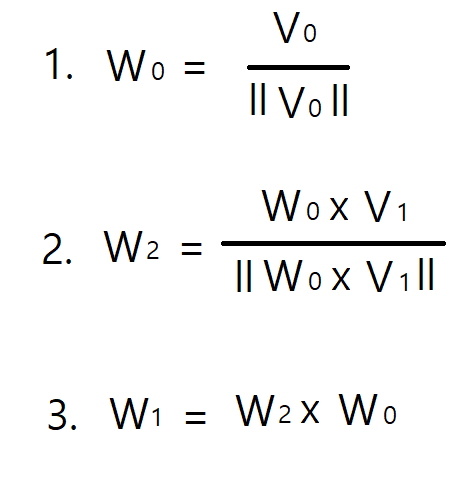
W2 ⊥ W0이고 ll W2 ll = ll W0 ll = 1 이므로 ll W2 x W0 ll = 1이다. 따라서 정규화는 필요하지 않다.
※ 점
- 3차원 그래픽 프로그램안에서는 어떤 물체의 위치를 지정할 수 있어야 된다.
그래서 벡터를 사용해서 위치를 나타내는데 , 벡터의 머리 끝 좌표를 이용하여 위치를 나타낸다. 이것을 위치벡터라 한다.
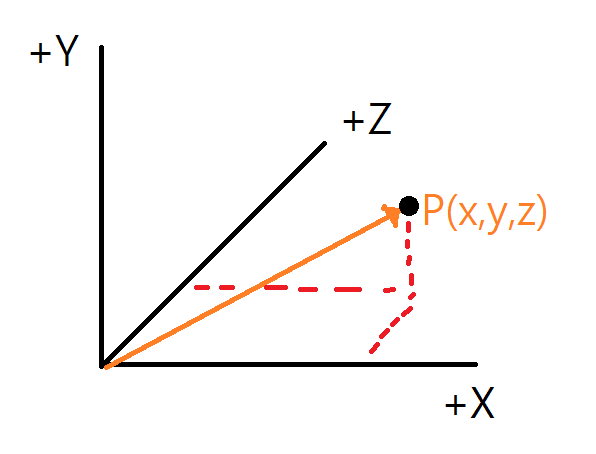
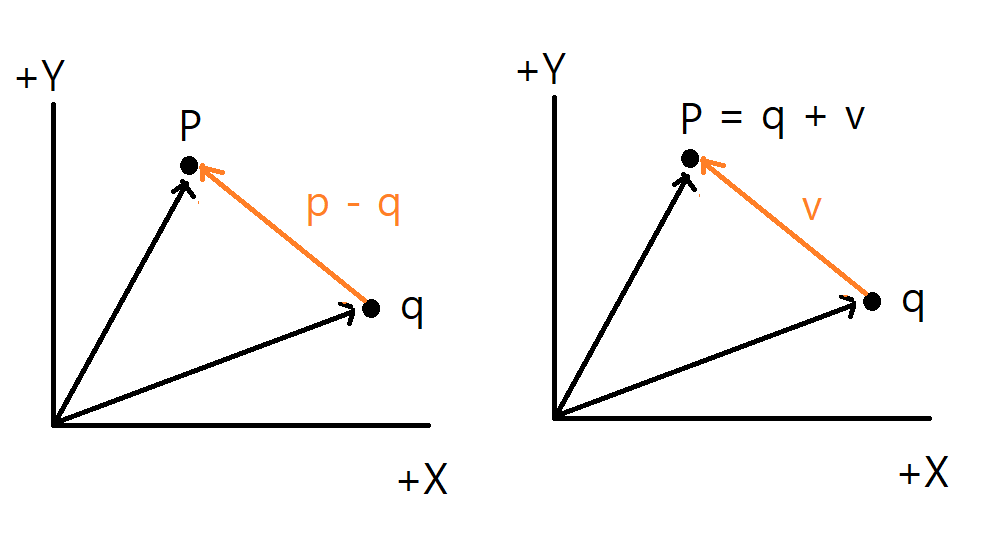
- 활용
점과 점 사이에 어느 방향으로 바라보고 있는지를 구할 때 사용한다.
끝
'Directx12 > 기본이론' 카테고리의 다른 글
| 전치행렬, 단위행렬, 행렬식, 딸림행렬, 역행렬 (0) | 2022.10.29 |
|---|---|
| 행렬 대수 (0) | 2022.09.05 |
| 내적, 직교투영 , 직교화 (0) | 2022.07.18 |
| 벡터의 길이와 단위벡터 (0) | 2022.07.17 |
| 벡터의 좌표 , 연산 (0) | 2022.07.15 |
내적, 직교투영 , 직교화
※ 내적
- 내적(inner product)은 점곱(dot product)이라고도 불린다.
표기법 ) U ● V
내적은 스칼라 값을 나타내는 벡터 곱셈이다. 곱셈 결과는 스칼라 값이 나온다.
다음과 같이 내적이 정의 된다.
U = (Ux , Uy, Uz) 인 벡터
V = (Vx , Vy , Vz) 인 벡터
U ● V = Ux Vx + Uy Vy + Uz Vz
실제계산)
U = (-1 , 3 , 6)
V = (-5 , 2 , 9)
U ● V = (-1 x -5) + (3 x 2) + (6 x 9) = 65
★ 내적의 정의만 봐서는 내적의 기하학적 의미가 분명하지 않다. 그래서 코사인 법칙을 적용하면
다음과 같은 관계를 찾을 수 있다.
U ● V = ll U ll x ll V ll x cosΘ
(여기서 Θ는 0 ≤ Θ ≤ π)
(U가 단위 벡터 , V가 단위 벡터 이면 U ● V = cosΘ 가 된다.)
- 여기서 유용한 속성 몇가지를 이끌어낼 수 있다.
1. U ● V = 0 이면 , U ⊥ V 이다 (수직이다. 즉 두 벡터는 직교이다.)
2. U ● V > 0 이면, 두 벡터 사이에 각도 Θ는 90도 보다 작다.
3. U ● V < 0 이면, 두 벡터 사이에 각도 Θ는 90도 보다 크다.
실제계산)
U = (1 , 2 , 3) 인 벡터
V = (-4 , 0 , -1) 인 벡터

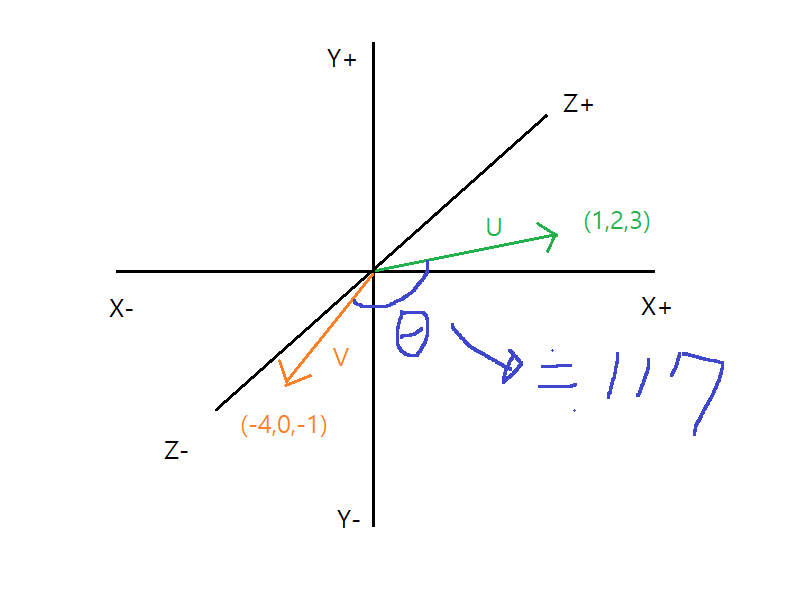
※ 직교투영
- 수직으로 내린 그림자 라는 뜻인데 어떤건지는 다음과 같이 보자.

★ 공식을 구해보자.
벡터 V , 단위벡터 n이 주어졌을 때 P를 내적을 이용해서 v와 n으로 표현하는 공식을 구해보자.

P = kn을 만족하는 스칼라 k가 존재
ll n ll = 1이므로
ll P ll = = ll kn ll = l k l x ll n ll = l k l
(P와 n이 반대 방향일 때 k는 음수를 가져서 절대값으로 나타낸다.)
이제 삼각함수 법칙들을 적용하면
COSΘ = k / ll v ll
k = ll v ll COSΘ
따라서
P = kn
P = (ll v ll COSΘ)n
그런데 n은 단위 벡터이므로 다음과 같이 표현
P = (ll v ll COSΘ)n
P = (ll v ll x 1 x COSΘ)n
P = (ll v ll x ll n ll x COSΘ)n
P = (V ● N)n
이 공식에 따르면 k = V ● N이다. n이 단위 벡터일 때 V ● N의 기하학적 의미를 말해준다.
이러한 P를 n에 대한 v의 직교투영(orthographic projection ; 또는 정사영)이라고 한다.
표기법)

※ 직교화(orthonormal)
- 벡터 집합{V0 ~ Vn-1}의 모든 벡터가 단위 길이고 , 서로 직교일 때 그러한 벡터 집합을 정규직교(orthonormal)집합이라 한다. (집합의 모든 벡터가 다른 모든 벡터와 수직이다.)
단, 주어진 벡터 집합이 정규직교에 가깝지만 완전히 정규직교가 아닌경우도 있다. 이러한 벡터 집합을 정규직교벡터 집합으로 만드는 걸 직교화(orthonormal) 이라고 한다.
- 왜 쓰는가?
최적화 하려고 쓴다고 한다. 예를 들어 어떤 벡터를 단위 벡터로 만들지 않고 쓰면 계산이 복잡해 진다. 즉 연산량이 많아진다. 그래서 크기 단위가 1인 벡터로 만들어 사용하면 연산이 적어진다. 고로 벡터 집합들을 단위 벡터로 다 모아두면 필요로한 벡터연산을 할 때 연산량을 적게 들이고 연산을 할 수 있다.
- 설명
다음 서로 직교인 2차원 벡터 집합을 만들어보자.
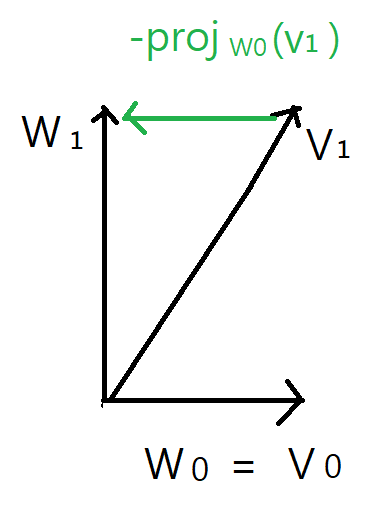
1. W0 = V0으로 시작해서 , 벡터 V1이 W0과 직교가 되게 만든다. 이를 위해 W0의 방향으로 작용하는 부분을 V1에서 뺀다.

이제 서로 직교인 벡터 집합 {W0 , W1} 이 만들어 졌다.
이제 집합을 정규화해서 단위 길이로 만들어 사용한다.
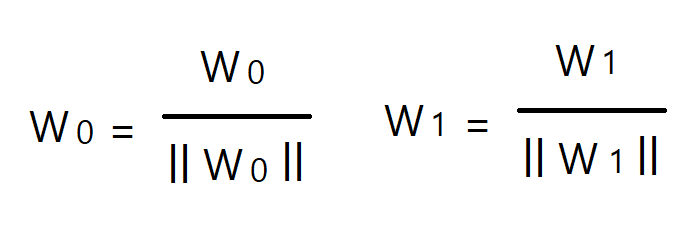
3차원도 비슷하다 단계만 늘어날 뿐이다.
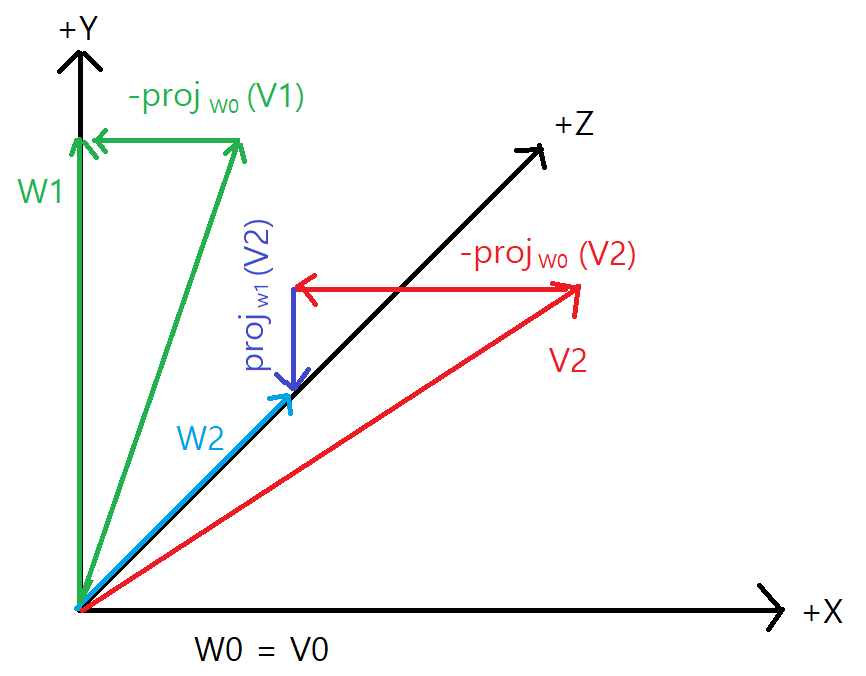
1. W0 = V0 시작 V1이 W0 직교되게 만든다. 이를 위해 W0 작용하는 부분을 V1에서 뺀다.
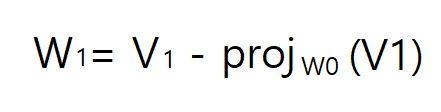
2. V2가 W0과 W1 모두에 직교가 되게 한다. 이를 위해 W0방향으로 작용하는 부분과 W1방향으로 작용하는 부분을 V2에서 뺀다.
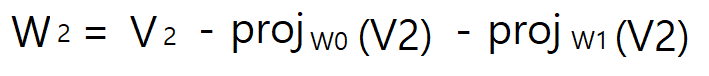
이제 서로 직교인 벡터 집합 {W0 , W1, W2} 가 만들어 졌다.
이제 이를 일반화해서 , N개의 벡터들의 집합 {V0 , V1 ... Vn-1}을 정규직교 집합 {W0,W1....Wn-1}으로
직교화 할때는 그람-슈미트 직교화라는 공정을 적용한다.

끝
'Directx12 > 기본이론' 카테고리의 다른 글
| 전치행렬, 단위행렬, 행렬식, 딸림행렬, 역행렬 (0) | 2022.10.29 |
|---|---|
| 행렬 대수 (0) | 2022.09.05 |
| 외적 , 직교화 , 점 (0) | 2022.07.21 |
| 벡터의 길이와 단위벡터 (0) | 2022.07.17 |
| 벡터의 좌표 , 연산 (0) | 2022.07.15 |
벡터의 길이와 단위벡터
1. 벡터의 크키(길이) 정의
- 기하학적으로 한 벡터의 크기는 해당 지향 선분의 길이이다. (지향 선분 : 방향이 있는 벡터)
표기법 : ll u ll

피타고라스 정리에 의해서

U 벡터의 크기(길이)가 나온다.
벡터의 크기(길이)는 알아봤다. 하지만 벡터는 순전히 방향만 나타내는 용도로만 쓰인다. 그래서 다음과 같이 길이가 1인 단위로 환산하여 단위벡터를 만들어서 사용한다.
2. 단위벡터(unit vector)
- 길이가 1인 단위로 만든 벡터. 길이가 1인 벡터로 만드는 것을 정규화(nomalization)이라고 한다.
다음은 정규화 공식이다.

- 공식 확인

- 계산
벡터 u = (-1 , 3 , 4) 정규화를 해보자

'Directx12 > 기본이론' 카테고리의 다른 글
| 전치행렬, 단위행렬, 행렬식, 딸림행렬, 역행렬 (0) | 2022.10.29 |
|---|---|
| 행렬 대수 (0) | 2022.09.05 |
| 외적 , 직교화 , 점 (0) | 2022.07.21 |
| 내적, 직교투영 , 직교화 (0) | 2022.07.18 |
| 벡터의 좌표 , 연산 (0) | 2022.07.15 |
벡터의 좌표 , 연산
벡터란 ?
1. Vector (방향량) 는 크기(magnitude)와 방향(direction)을 모두 가진 수량(quantity)을 가리키는 말이다.

벡터의 예)
1. 힘(force) : 특정한 힘의 세기(크기) & 방향
2. 변위(displacement) : 한 입자의 최종적인 이동 방향 & 거리
3. 속도(velocity) : 빠르기 & 방향
따라서 힘,변위,속도를 나타낼 때 벡터를 씀.
1) 벡터와 좌표계 표현
2차원 벡터의 표현

(a,b)의 방향을 가진 벡터
3차원 벡터의 표현(왼손좌표계를 사용)

(a,b,c)의 방향을 가진 벡터
2) 벡터의 연산
하나의 벡터 U로 지칭하고 U = (Ux,Uy)로 정의하겠음.
하나의 벡터 V로 지칭하고 V = (Vx,Vy)로 정의하겠음.
(여기선 표현하려고 2차원 벡터로 표현 , 3차원도 똑같이 적용됌.)
- 덧셈
U + V = (Ux + Vx , Uy + Vy)
ex) U = (3,2)
V = (2,3)
U + V = (3+2 , 2+3) = (5,5)

- 뺄셈
U - V = (Ux - Vx , Uy - Vy)
ex) U = (3,2)
V = (2,3)
U + V = (3-2 , 2-3) = (1,-1)

- 스칼라 곱셈
스칼라란 ? 벡터를 곱할 수 있는 양
스칼라를 K라 칭함
하나의 벡터 U에 스칼라를 곱함, U = (kUx , kUy)로 정의하겠음.
k = 5
U = (2,3)
kU = (5x2 , 5x3) = (10, 15)

'Directx12 > 기본이론' 카테고리의 다른 글
| 전치행렬, 단위행렬, 행렬식, 딸림행렬, 역행렬 (0) | 2022.10.29 |
|---|---|
| 행렬 대수 (0) | 2022.09.05 |
| 외적 , 직교화 , 점 (0) | 2022.07.21 |
| 내적, 직교투영 , 직교화 (0) | 2022.07.18 |
| 벡터의 길이와 단위벡터 (0) | 2022.07.17 |
다이렉트12 예제 실행 시 에러 대처

이 책의사서 공부하면 예제를 만든 아래의 사이트를 준다.
https://github.com/d3dcoder/d3d12book
GitHub - d3dcoder/d3d12book: Sample code for the book "Introduction to 3D Game Programming with DirectX 12"
Sample code for the book "Introduction to 3D Game Programming with DirectX 12" - GitHub - d3dcoder/d3d12book: Sample code for the book "Introduction to 3D Game Programming with Direc...
github.com
이걸 사용하는 버전은 Visual studio 2015인데 내가 사용하는 버전은 Visual studio 2019버전이다.
여기서 세 가지 문제점이 나타났다.
문제 1. Box예제를 그대로 옮겨 왔는데 다음과 같은 문제점이 나타났다.

&에 l-value가 있어야 된다는 오류다.
- 해결방법

준수모드를 "기준값"으로 바꿔주면 된다.
문제2.

이러한 에러가 났다.
-해결방법
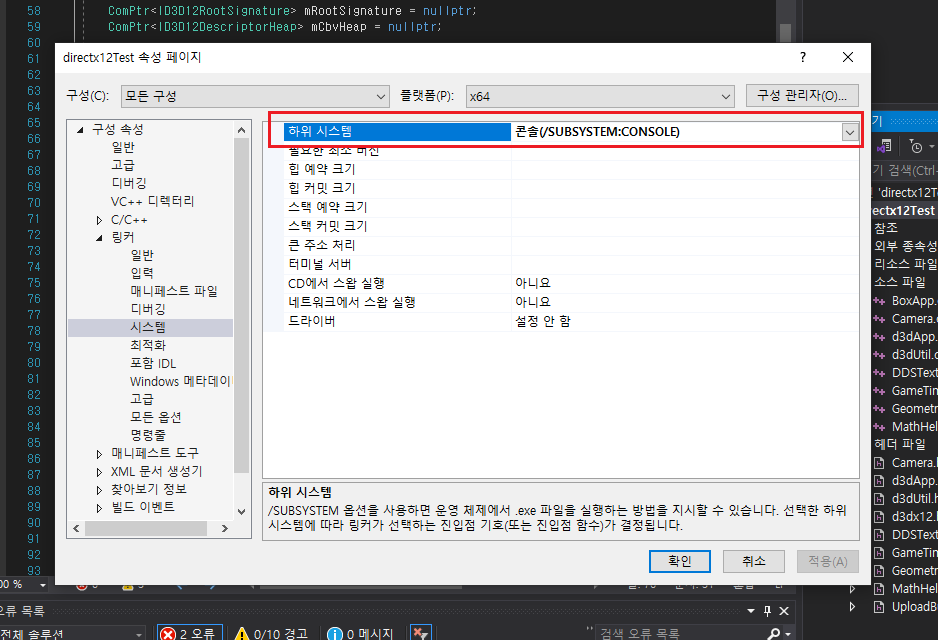
콘솔로 되어있을 것이다.
창으로 바꾸면 된다.
문제3.
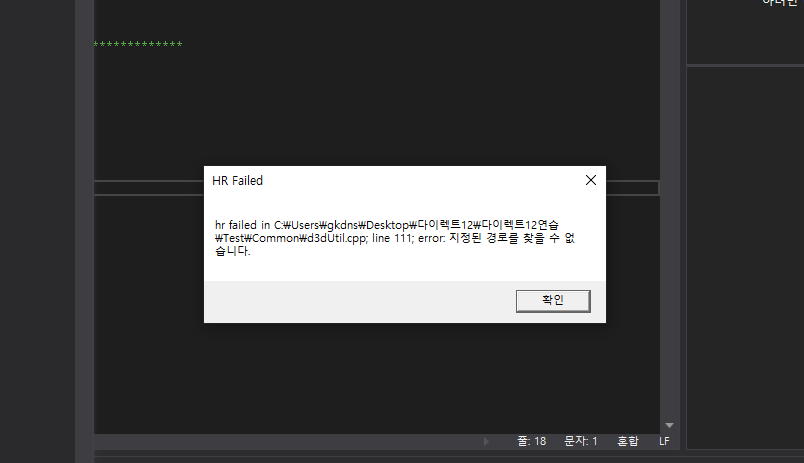
이러한 에러가 났다.
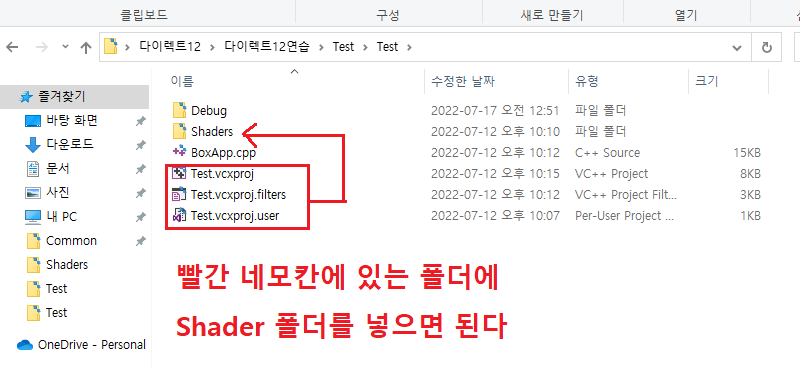
-해결방법
Shader 폴더 위치 때문에 생김