※ 행렬 사용 이유
▶ 3차원 컴퓨터 그래픽에서 행렬은 비례나 회전, 이동 같은 기하학적 변환을 간결하게 서술하는 데 쓰이며, 점이나 벡터의 좌표를 한 기준계에서 다른 기준계로 변환하는 데에도 쓰인다.
※ 정의
▶ m x n 행렬 M은 m개의 행과 n개의 열로 이루어진 실수들의 정사각 배열이다. 행(row)들의 개수와 열(column)들의 개수의 곱(이를테면 4x4)을 행렬의 차원이라고 부른다. 행렬을 구성하는 수들을 성분(entry) 또는 원소(element; 또는 요소)라고 부른다.
행렬의 한 성분을 나타낼 때에는 다음과 같이 나타낸다.

i는 행, j는 열이다.
▶ 다음 행렬들을 생각해 보자.

1. A = 4 x 4 행렬 , B = 3 x 2 행렬, u = 1 x 3 행렬, v = 4 x 1 행렬이다.
2. 행렬 A의 4행(넷째 행) 2열(둘째 열)의 성분(-5)을 A₄₂라고 표기한다.
3. 행렬 u , v는 각각 행과 열이 하나라는 점에서 특별한 행렬이다. 이런 종류의 행렬을 행벡터와 열벡터라고 부른다. 이것은 벡터를 행렬 형태로 표기할 때 쓰이기 때문이다. (예를 들어 벡터( x , y , z)를 행렬[ x , y , z]로 맞바꾸어 사용할 수 있다.)
▶ 종종 한 행렬의 행들을 벡터로들로 간주하는 것이 편리할 때가 있다. 예를 들어 행렬을 다음과 같이 표기할 수도 있다.


# 행렬의 상등, 덧셈, 스칼라 곱셈, 뺄셈 연산을 정의
1. 두 행렬은 오직 대응되는 성분들이 상등일 때에만 상등이다.(두 행렬의 상등을 비교하려면 두 행렬의 행 개수들, 열 개수들이 같아야 된다.)
2. 두 행렬을 더할 때에는 대응되는 성분들을 더한다. 따라서 차원이 같은 행렬들만 더할 수 있다.
3. 행렬에 하나의 스칼라를 곱할 때에는 행렬의 모든 성분에 그 스칼라를 곱한다.
4. 행렬의 뺄셈은 스칼라 곱셈과 행렬 덧셈으로 정의한다. 즉 (A - B = A + (-1 x B) = A + (-B))이다.
▶ 행렬 덧셈과 스칼라 곱셈은 성분별로 이루어지므로, 행렬 덧셈과 스칼라 곱셈도 실수의 덧셈 및 곱셈의 다음과 같은 성질들을 만족한다.

※ 행렬 곱셈
# 정의 : 만일 A가 m x n 행렬이고 B가 n x p 행렬이면 둘의 곱 AB가 정의된다. 곱 AB는 하나의 m x p 행렬이다. 이를 C라고 할 때 , C의 ij번째 성분은 A의 i번째 행벡터와 B의 j번째 열벡터의 내적이다. 즉,
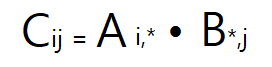
이다. 따라서 행렬 곱 AB가 정의되려면 A의 열 수와 B의 행수가 같아야 된다. 다른 말로 하면, A의 행벡터들의 차원과 B의 열벡터들의 차원이 같아야 된다. 이 차원들이 일치 하지않으면 내적이 말이 안된다.
Ex 1)
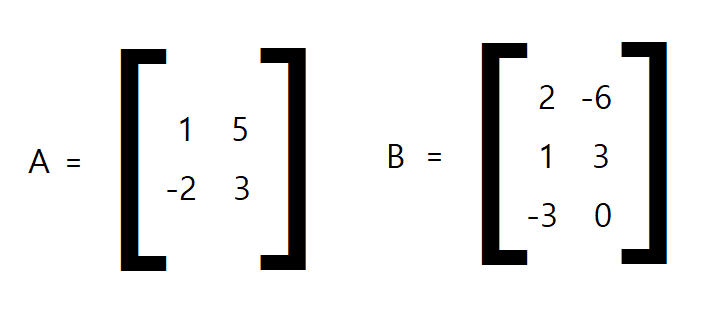
▶ A의 행벡터들의 차원은 2이지만 B의 열벡터들의 차원은 3이므로, 두 행렬의 곱 AB는 정의되지 않는다. 좀 더 구체적으로, A의 첫 행벡터와 B의 첫 열벡터의 내적을 취할 수가 없다. 2차원 벡터와 3차원 벡터의 내적을 취할 수 없기 때문이다.
Ex 2)
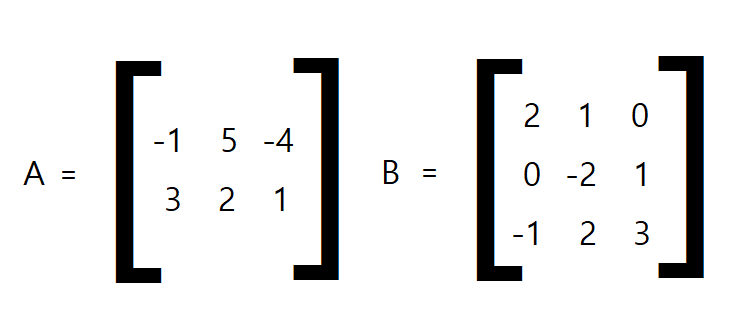
▶ 이 경우에는 곱 AB가 정의된다. A의 열 수와 B의 행 수가 같기 때문이다.
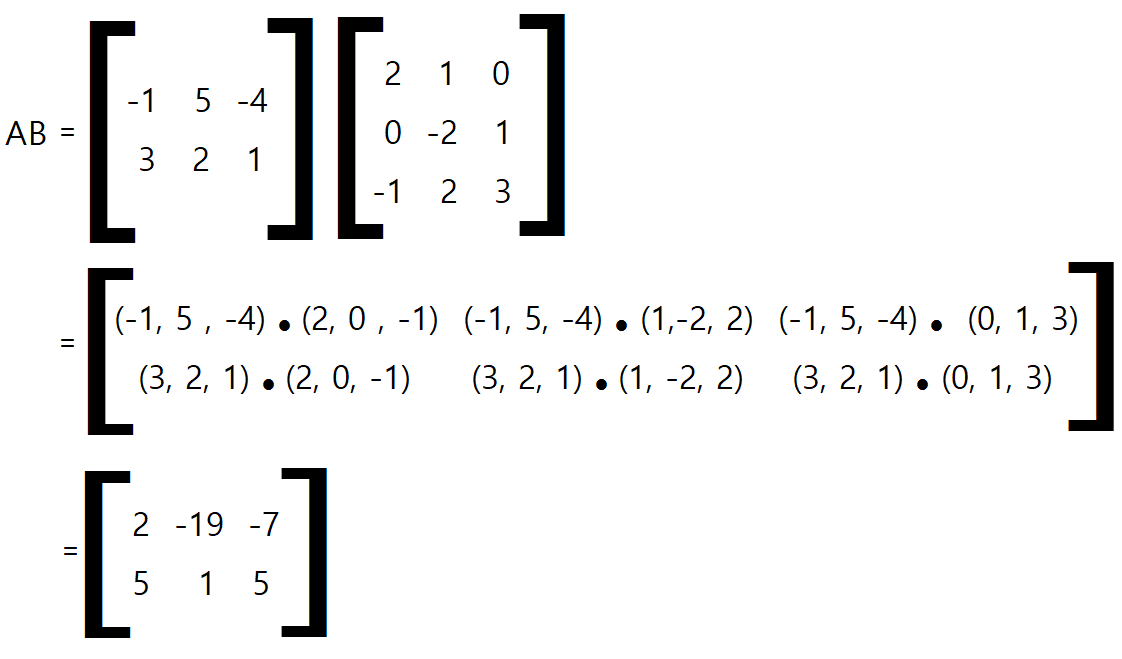
곱 BA는 정의되지 않음을 주목하기 발나다. B의 열 수와 A의 행수가 같지 않기 때문이다. 이 예에서 보듯이, 일반적으로 행렬 곱셈에는 교환법칙이 성립하지 않는다. 즉 AB ≠ BA이다.
# 벡터와 행렬의 곱셈
다음과 같은 벡터 x 행렬 곱셈을 생각해 보자.
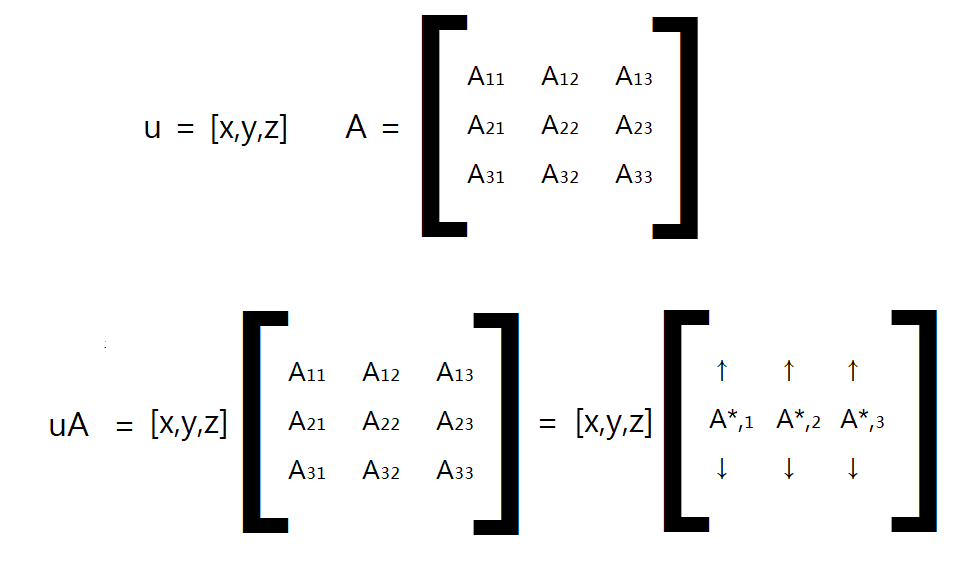
이 경우 uA가 1 x 3 행벡터로 평가됨을 주목하기 바란다. 위의 내용을 다음 행렬곱셈으로 적용하면 다음과 같이 나온다.
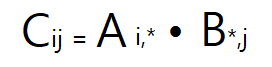

이 것은 선형결합(linear combination, 일차결합)의 한 예이다. 이 식은 벡터 x 행렬 곱 uA가 행렬 A의 행벡터들과 벡터 u로 주어진 스칼라 계수 x , y , z의 선형결합에 해당함을 말해준다. 이 예는 1 x 3행벡터와 3 x 3 행렬의 경우이지만, 앞의 문장은 일반적으로도 참임을 주목하기 바란다. 즉 , 어떤 1 x n 행벡터 u와 어떤 n x m 행렬 A에 대해, 곱 uA는 A의 행벡터들과 u의 스칼라 계수들의 선형결합이다.
# 결합법칙
행렬 곱셈에는 몇 가지 편리한 대수적 성질들이 존재한다. 예를 들어 행렬 곱셈은 덧셈에 대한 분배법칙을 만족한다. 즉, A(B + C) = AB + AC이고 (A + B)C = AC + AB이다. 더욱 중요한 것은, 행렬 곱셈이 다음과 같은 결합법칙을 만족한다는 것이다.
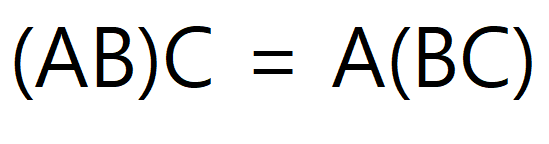
'Directx12 > 기본이론' 카테고리의 다른 글
| 회전변환 식 유도 잘나온 사이트 (0) | 2022.11.22 |
|---|---|
| 전치행렬, 단위행렬, 행렬식, 딸림행렬, 역행렬 (0) | 2022.10.29 |
| 외적 , 직교화 , 점 (0) | 2022.07.21 |
| 내적, 직교투영 , 직교화 (0) | 2022.07.18 |
| 벡터의 길이와 단위벡터 (0) | 2022.07.17 |