※ 외적(Cross dot 또는 Outer product)
- 외적은 벡터와 벡터를 곱하면 내적과 달리 벡터가 나온다. (내적은 스칼라 값이 나온다.)
오직 3차원 벡터에서만 정의 된다. (2차원은 x)
두 3차원 벡터 u , v를 외적을 취하면 u,v 모두에 직교인 또 다른 벡터 w가 나온다.
- 정의
U x V 일 때


V x U 일때


W가 외적 방향이다.
왼손 좌표계 적용시 두벡터를 반대로 곱하면 새로 나오는 벡터가 뒤집어 진다.

- 계산해보면
U = (2 , 1 , 3) , V = (2 , 0 , 0) 할 때 , W = U x V 와 Z = V x U를 비교하교 직교임을 확인해보자.
W = U x V
W = ( (1 x 0) - (3 x 0) , (3 x 2) - (2 x 0) , (2 x 0) - (1 x 2) )
W = (0 , 6 , -2)
Z = V x U
Z = ( (0 x 3) - (0 x 1) , (0 x 2) - (2 x 3) , (2 x 1) - (0 x 2))
Z = (0 , -6 , 2)
이 결과 U x V ≠ V x U 라는 사실을 알게된다.(외적은 교환 법칙 성립 X)
U x V = -V x U 는 된다.
W가 U또는 V에 직교임을 확인하는 방법은 W●U , W●V 내적을 해서 0이 나오면 서로 직교이다.
- 계산해보면
W●U = WxUx + WyUy + WzUz(공식)
W●U = (0 , 6 , -2) ● (2 , 1, 3)
W●U = (0x2) + (6 x 1) + (-2 x 3) = 0
W●V = (0 , 6 , -2)●(2 , 0 , 0)
W●V = (0x2) + (6x0) + (-2 x 0) = 0
직교임을 알 수 있다.
※ 직교화
- 내적에서 그람슈미트 공정을 통한 직교화를 알아봤다. 여기서는 다른 공정을 통해서 직교화를 구해본다.
다음 공정을 진행한다.

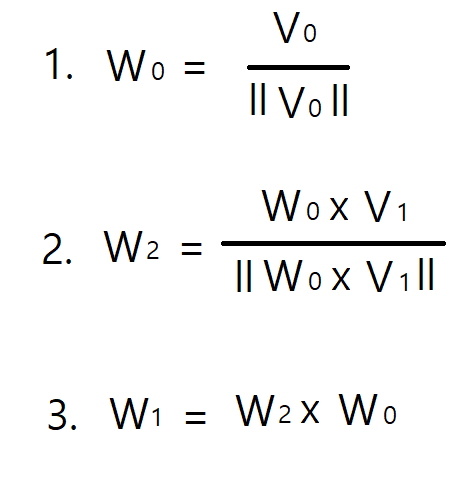
W2 ⊥ W0이고 ll W2 ll = ll W0 ll = 1 이므로 ll W2 x W0 ll = 1이다. 따라서 정규화는 필요하지 않다.
※ 점
- 3차원 그래픽 프로그램안에서는 어떤 물체의 위치를 지정할 수 있어야 된다.
그래서 벡터를 사용해서 위치를 나타내는데 , 벡터의 머리 끝 좌표를 이용하여 위치를 나타낸다. 이것을 위치벡터라 한다.
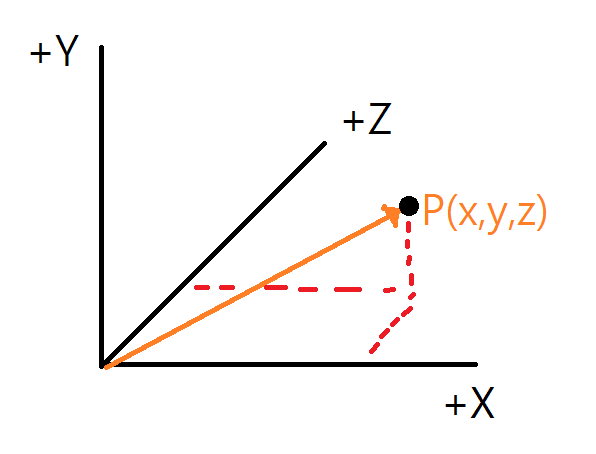
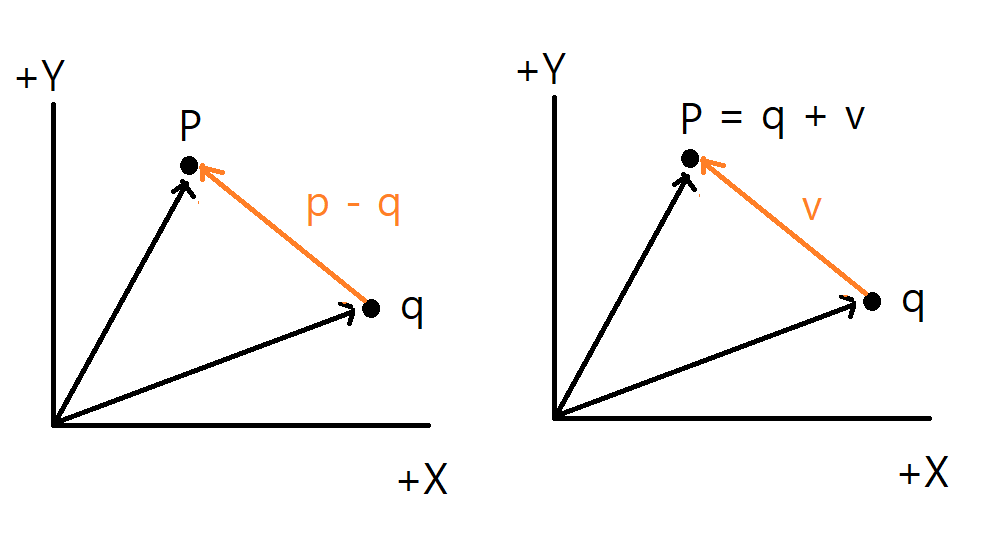
- 활용
점과 점 사이에 어느 방향으로 바라보고 있는지를 구할 때 사용한다.
끝
'Directx12 > 기본이론' 카테고리의 다른 글
| 전치행렬, 단위행렬, 행렬식, 딸림행렬, 역행렬 (0) | 2022.10.29 |
|---|---|
| 행렬 대수 (0) | 2022.09.05 |
| 내적, 직교투영 , 직교화 (0) | 2022.07.18 |
| 벡터의 길이와 단위벡터 (0) | 2022.07.17 |
| 벡터의 좌표 , 연산 (0) | 2022.07.15 |